Figure: Minimax Search Tree: Backed-up score shown in nodes

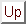

The minimax algorithm is a method of selecting the best choice of action in a situation, or game, where two opposing forces, or players, are working toward mutually exclusive goals, acting on the same set of perfect information about the outcome of the situation. It is specifically applied in searching game trees to determine the best move for the current player of a game. It uses the simple principle that at each move, the moving player will choose the best move available to them.
The game tree consists of all moves available to the current player as children of the root, and then all moves available to the next player as children of these nodes, and so forth, as far into the future of the game as desired. Each branch of the tree represents a possible move that player could make at that point in the game. Evaluating the game at a leaf of this tree yields the projected status of the game after that sequence of moves is made by the players. A deeper search of the game tree provides more information about possible advantages or traps and therefore yields a better move.
In a situation, like Othello, with two players, Black and White, Black values moves with high evaluation scores and White values moves with low evaluation scores. A minimax search determines all possible continuations of the game to the desired level, evaluating each possible set of moves and assigning a score. The search then steps back up through the game tree and alternates between choosing the highest child score at nodes representing Black, and the lowest child score at nodes representing White. The score returned is called the ``backed up'' score since it is chosen by backing up through the tree. Thus, stepping through the game tree is equivalent to examining alternating moves between Black and White. Such a forward looking search is beneficial because Black might make a fantastic move at one level, only to allow White to make a move that can be oppositionally fantastic. By looking ahead in this way, Black can make moves that are advantageous, but that don't allow White to make moves negating such benefit.
Figure 1 shows a tree simulates the progression of a game through the next four moves, with Black as the current player. As shown, while Black could possibly obtain higher scores by choosing moves that lead to the left or right trees, those moves expose Black to the risk that White will make moves that lead to the lower scores. Therefore, while the goal score is not the overall optimal score possible after 4 moves, it is the optimal score when White's motives are taken into account.

Figure: Minimax Search Tree: Backed-up score shown in nodes
The minimax algorithm is a recursive algorithm that takes as arguments the current layout of the game board, the depth being searched, and the maximum depth to be searched. It returns the chosen move, and the score that such a move might lead to. The algorithm has a two part base case and then calls minimax on the boards resulting from each possible move at the current level.
The base case of the algorithm evaluates the score for the given board. This occurs in two situations. First, the board will be evaluated if the current depth of the search is the maximum desired depth. Second, the board will be evaluated if there are no possible moves for either player, signaling a possible end to the game.
Should there be moves for the current player and the maximum depth hasn't yet been searched, minimax generates possible moves at that level, and applies them in turn to the current board, calling minimax on the resulting board. Each returned score is compared to the current best. If the returned score is more advantageous for the current player, that score replaces the best score and the move that generated it replaces the best move.
minimax(in game board, in int depth, in int max_depth,
out score chosen_score, out score chosen_move)
begin
if (depth = max_depth) then
chosen_score = evaluation(board);
else
moves_list = generate_moves(board);
if (moves_list = NULL) then
chosen_score = evaluation(board);
else
for (i = 1 to moves_list.length) do
best_score = infinity;
new_board = board;
apply_move(new_board, moves_list[i]);
minimax(new_board, depth+1, max_depth, the_score, the_move);
if (better(the_score, best_score)) then
best_score = the_score;
best_move = the_move;
endif
enddo
chosen_score = best_score;
chosen_move = best_move;
endif
endif
end.
Since the amount of work a minimax search generates increases exponentially as a move is examined to a greater depth, to reduce the time required for the search it must be restricted so that no time is wasted searching moves that are obviously bad for the player. One key way to do this is to implement alpha-beta cutoffs in the minimax search. Alpha-beta cutoffs work on the previously discussed principle that a player, Black, will not make a seemingly good move if it allows White to make an even better move. Thus, if while examining moves, a move is found with a score worse than the best score now guaranteed, the algorithm will discontinue the search of that branch of the tree. The exact implementation of alpha-beta keeps track of the best move for each side as it moves through the tree. If a move is evaluated that is advantageous for the current player but not for the opponent, then the rest of the moves in the tree are discarded because progressing to that state would not be allowed by one of the players.
Using alpha-beta cutoffs can cause immense speedups in the run of minimax by reducing the size of the tree that must be searched. To illustrate this, Figure 2 shows the above minimax tree adjusted with alpha-beta cutoffs is shown below. The cutoffs reduce the search by 10 nodes, cutting the necessary time by about 30%.
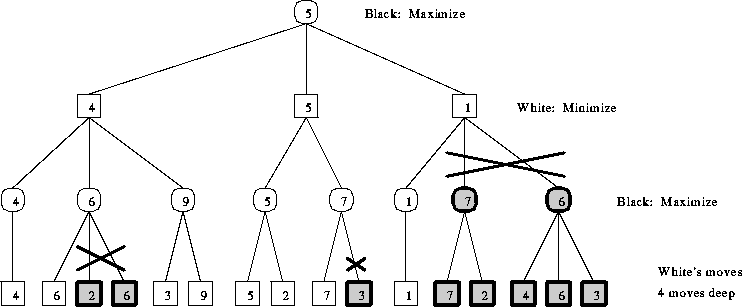
Figure: Minimax Search Tree with Alpha-Beta cutoffs: cutoff nodes are shaded
Note: Here Black prefers high scores and White prefers low scores.
minimax (in game board, in int depth, in int max_depth,
in boolean alpha_beta, in score black_best, in score white_best,
out score chosen_score, out score chosen_move)
begin
:
:
minimax(new_board, depth+1, max_depth,
alpha_beta, black_best, white_best,
the_score, the_move);
if (alpha_beta) then
if (to_move(black) and (the_score > black_best))
if (the_score > white_best)
break; /* alpha_beta cutoff */
else
black_best = the_score;
endif
endif
if (to_move(white) and (the_score < white_best))
if (the_score < white_best)
break; /* alpha_beta cutoff */
else
white_best = the_score;
endif
endif
endif
:
:
end.
Any implementation of minimax and alpha-beta must be supplied with the following types and routines.